COURSE DIRECTOR	CLASSES (see also Lecture Schedule Information)
G. Tourlakis	Thursdays
Room 354, CCB	6:00-9:00 p.m.
Telephone: 736-2100-1-66674	Classroom: 120, CCB
e-mail: gt@cs.yorku.ca	York Campus

Computer Science mainly involves the design, analysis, and implementation of algorithms. An algorithm, roughly speaking, is a book-keeping procedure which when applied to a class of inputs will perform a sequence of well defined steps to yield eventually, for each such input, a corresponding output.

In COSC 4021.03 our first concern will be to give a precise definition to the word "algorithm". The approach is, more or less, to say that an algorithm is any process implemented (or implementable) on a computer.

It turns out that one must be very careful with the use of the word "computer". For example, is there an algorithm which for any will compute the decimal representation of the following function?

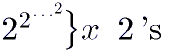
If we adopt the above suggestion as a definition of an algorithm, then there is no "algorithm" to compute 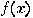for any, except trivially small .

This however is counter-intuitive: Clearly there is an effective or "mechanical" procedure which, given enough time and enough space to hold the answer, could carry out the computation of 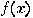for any . This example suggests that although it is reasonable to require from an algorithm to be a "mechanical" procedure, it is unwise to base a formal definition on technology dependent actual machines. The way it is often done is to define first a class of  "abstract computers" or "machines", e.g., Turing Machines, and then say that an algorithm is any procedure implementable on such a machine.

Informally, a Turing Machine is a mathematical abstraction of a computer. In other words, while the main features have been retained, namely the ability to go unambiguously from one computation step to the next, the technology dependent features have been discarded: For example, unlike a "real" computer, a Turing Machine has an infinitely extendable "memory".

Given the definition of an algorithm, the next question to be asked is "what is computable?"

We know from experience that quite a few interesting problems are "programmable", i.e., computable. We will also encounter quite a few interesting problems which are not computable. For example, we shall see that a general "program" which tests the correctness of arbitrary programs cannot (and does not) exist.

The above issue, "what is computable", is the central theme of the general Theory of Computability (otherwise known as Recursion Theory). Studying the general computable functions of this theory is very enlightening and helps towards our understanding of the computational processes in general. Moreover, this theory finds some startling applications in Logic, where we shall see that there are "true" elementary arithmetic statements which nevertheless are not provable "rigorously" (Gödel’s Incompleteness Theorem).

It can be said that COSC 4021.03 provides the student with the theoretical foundation of what he/she has learnt in courses on theory of computation, analysis of algorithms, data structures, compilers, etc.
The topics in the course will be chosen from (roughly in the indicated sequence):

Primitive Recursive functions and relations, Loop-Programs, Elementary Functions, Turing Machines, Computable and semi-Computable functions and relations, Church’s Thesis, arithmetization of Turing Machines and the Kleene predicate, Unsolvable Problems, Recursion Theorem, Rice’s Theorem, Reducibilities, Productive and Creative sets and Gödel’s Incompleteness Theorem.

Prerequisite.

The essential prerequisite for COSC 4021.03 is a certain degree of proficiency in following and formulating combinatorial arguments. Such proficiency should be normally acquired by a student who has successfully completed a course such as COSC 2001.03 (AK/COSC 3431.03) and at least one of MATH 1090.03 or MATH 2441.03.
Students who have not completed any of the above courses, but believe that they have the equivalent background, should seek special permission to enroll, in consultation with the instructor.

Work-Load and Grading.

The course grade will be based mainly on about 3-4 homework assignments. There will be no programming problems, but each assignment will consist of a number of theoretical problems; for example "prove that such-and-such function is not computable", or "prove that such-and-such function is primitive recursive", etc.

Textbook.

G. Tourlakis, Computability, Reston Publishing Company.
NB. The text will be made available via the Reserve Library since it is out of print.

References.

(1) J.E. Hopcroft and J.D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley.
For more on Primitive Recursive and (total) Recursive functions see:
(2) R. Péter, Recursive Functions, Academic Press (Number-theoretic approach, rigorous, fairly difficult).
For more on unsolvability of concrete problems of combinatorial or number theoretical nature, see:
(3) M. Davis, Computability and Unsolvability, McGraw-Hill (Turing approach, rigorous, fairly difficult).
Matijasevic’s proof of the unsolvability of Hilbert’s 10th problem, using methods initiated by Davis in (3) can be found in:
(4) Y.I. Manin, A Course in Mathematical Logic, Springer-Verlag (quite difficult).
For more on recursion theory, in general, see:
(5) H. Rogers, Theory of Recursive Functions and Effective Computability, McGraw-Hill (Semi-formal—using Church’s thesis—throughout, difficult).
Finally, for more on machines at an elementary level, see:
(6) M. Minsky, Computation; Finite and Infinite Machines, Prentice-Hall. __