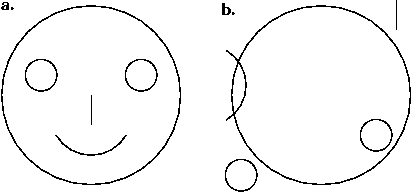Introduction

1. Introduction

Our visual perception system is capable of determining abstract  properties of shapes and objects as well as any spatial relations which may exist amongst them.  This ability is a fundamental requirement of the visual recognition system.  For example, consider the two circles (A and B) illustrated in figure 1.  It is effortlessly determined (or so it appears) that the diameter of circle that the diameter of circle B is greater than the diameter of circle A.
 
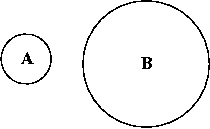Figure 1.  Two circles (A, B) with different diameters.  The diameter of circle B is clearly larger than the diameter of circle A.

As a further example, consider figure 2a,b.  The image of figure 2a is easily recognized as a face although it consists of only several primitive shapes (which do not even correspond to the shape of actual face parts - for example, our nose is not a straight line and our eyes are not perfectly round), contains no texture or color.  However, by simply re-arranging the four shapes comprising the eyes, nose and mouth, the image of figure 2b is certainly not recognized as a face.  Such relations are easily determined by our visual system and appear to occur immediately without any awareness.  However the certainly is no magic involved, and although we may not be aware of it,  there are some complex  operations taking place to determine relationships between objects such as the ones described above.
 

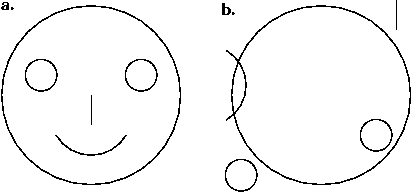Figure 2.  The shapes comprising the image of figure a are easily perceived as a face.  The same shapes are not longer recognized as a face when they are re-arranged as in figure b.

The purpose of this paper is to present and examine several operations which may be responsible for determining abstract relations amongst shapes and object.  In particular, ipresents a set of elemental operations which may be combined to meet specific goals by the visual perceptual system.

1.1 Perception of Inside / Outside Relations

Inside / outside relations allow for the ability of determining whether some object (or objects) are within (inside) or out of (outside) some other object or shape.  For example, referring to figure 3a below, it is easily determined that the red circle (target) is inside the polygon.  Similarly, in figure 3b, the red target is outside of the polygon.  Determining such relationships appears very easy to us, especially with such simple objects and targets Although it may appear that such relations are determined immediately and without any effort even more with complex shapes as in figure 3c, this is clearly not the case!  There are actually many complex processes involved, despite this effortless appearance, which we may not necessarily aware of.  Furthermore, according to the author, the processes involved are not entirely known.  Inside / outside relations can also be determined algorithmically using computers.  However, the algorithms currently available come nowhere near the ability of the human system.  These algorithms "break-down" in many circumstances, require more time to compute and unlike the human system, these algorithms do not scale with the "size" of the input.  The following sections describe two algorithms developed (and implemented - see [2], [6]) to compute inside / outside relationships.
 
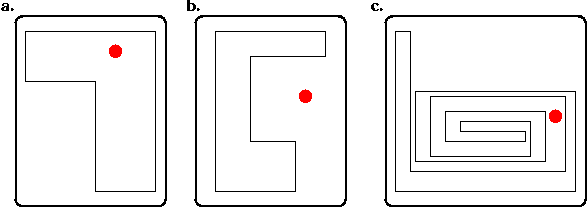Figure 3.  Inside / Outside Relationships. 

1.1.1 Ray Tracing

As illustrated in figures 4a,b, in the ray tracing method, a "ray" (line) is drawn from the target to "infinity" (of course the line is not really extend to infinity but rather, to the limits of our workspace or far enough such that we know there are no other objects etc.).  The number of intersections between the ray and the shape in question determines whether the target is inside or outside.
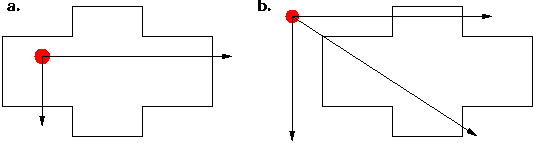Figure 4.  Ray Intersection Method.  Target is inside the polygon (figure a) and target is outside the polygon (figure 4b).

As mentioned above, the ray intersection method can easily "breakdown" and will work only under certain conditions.  For example, the curve must be "closed" (see figure 5a) and there must not be any other shapes (objects) in the path of a ray (see figure 5b).  Given these limitations, the author concludes that the human system does not employ ray intersection, and the method it does use is superior to the ray intersection method.
 

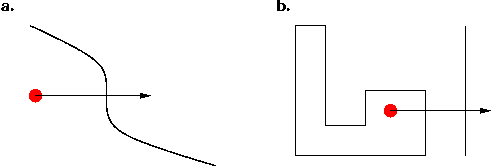Figure 5.  Breakdown of the Ray Intersection Method.

1.1.2 Coloring

With the coloring method, as shown in figure 6, starting at some point, the area surrounding it is activated or "colored" (e.g. somehow it is recorded that this area has been visited).  We continue coloring until a border is encountered.   Basically, if the coloring reaches some point at infinity, the target is not inside the shape.  However, if the coloring process completely stops before reaching some area surrounding some point at infinity, then the target is inside the shape .
 
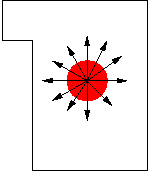Figure 6.  Coloring Method.

Although the coloring method does overcome some of the limitations associated with the ray tracing method, it still has its share of shortcomings and once again, the human system is superior.  For example, the coloring method will also fail when the shape is not closed.