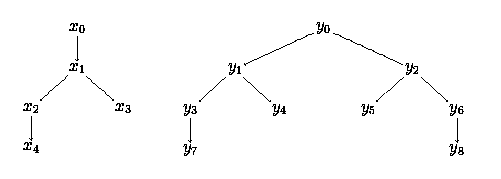

Discrete probabilistic transition systems are considered to behave the same if they are probabilistic bisimilar. For example, the probabilistic transition systems
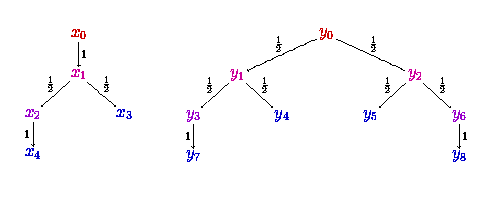
For probabilistic systems qualitative information, like probabilistic bisimilarity, is often too restrictive in practice and a (complementary) quantitative approach to verification is needed. For instance, the probabilistic transition systems
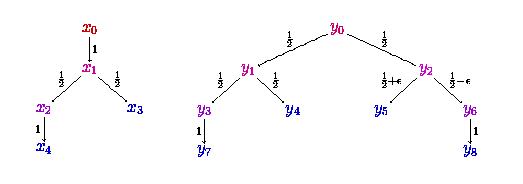
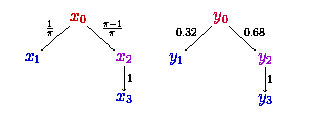
In a quantitative approach to verification, answers to questions like ``What is the probability that the system satisfies its specification?'' and ``Do the systems behave almost (up to some small fluctuations) the same?'' provide us with (often more useful) quantitative information about the systems. In my current research, the latter kind of questions are addressed.
The difference in behaviour of systems can be naturally captured by means of a pseudometric. It provides a quantitative notion of behavioural equivalence. A pseudometric differs from an ordinary metric in that different states may have distance 0. The distance between (initial) states of probabilistic transition systems, a real number between 0 and 1, expresses the similarity of the behaviour of the systems. The smaller the distance, the more alike the systems behave. Systems behave almost the same, up to ε-fluctuations, if their distance is at most ε. Furthermore, the distance between systems is 0 if they are indistinguishable, that is, they are probabilistic bisimilar.
This research is supported by the Natural Sciences and Research Council of Canada.
