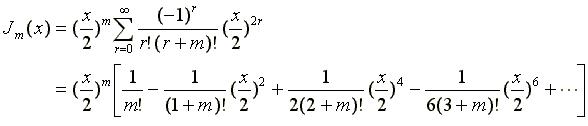
y at a given
x in terms of standard functions and operators. One example is
the Bessel
function of the first kind, defined as: 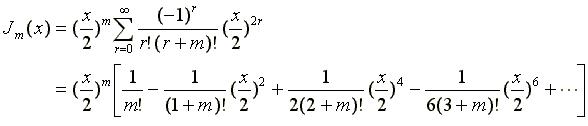
m, we get a different Bessel
function so the above series defines in fact a family of Bessel functions. These
functions appear as solutions to integral and differential equations in diverse
scientific fields and are considered as natural extensions of
trigonometric functions like sin and cos. In this Lab,
we focus on J1(x), the Bessel function of the first kind
of order 1 (obtained by substituting m = 1 in the above) and seek
to chart it in the range [0,10].
m = 1 and write out the first 6 or seven
terms in the series. Try to see a pattern that allows one to compute each term
from its predecessor; e.g. ask yourself: if I was told that the 4th term is
0.725 and was given the value of x, how do I compute the 5th term? You can, of course,
compute the 5th term from scratch but we prefer an incremental approach.
x, a
real*8 number and compute the sum of the series. The loop should
keep computing and accumulating terms until the absolute value of the term to
be added becomes less than some EPSILON. Make sure that all computations
are done using real*8 and/or integer*2; i.e. do not
allow real*4 round-off errors.
EPSILON to 1.E-3.
J1(0). The answer should be
0, and if not, debug your program.
J1(10). The answer should be
about 0.04; if not, debug your program.
EPSILON is changed to 1.E-6?
EPSILON is changed to 1.E-15?
x. Instead, it
sets up a loop that generates 21 values for x, ranging from 0 to
10
in increments of 0.5.
The output must show the value of x and
the corresponding value of J1(x) in a tabular fashion;
e.g.
0.0 0.000000000
0.5 0.242268458
...
...
9.5 0.161264431
10.0 0.043472746
(use a small value of EPSILON, like 1.E-12, and format the
output so that 9 decimals are shown.)
bessel.txt.
bessel.txt.
Note that Excel can read multi-column text files if they have fixed sizes (the
columns are aligned) or if they are delimited (a space or a tab separates the
columns). Our file has fixed-size columns that are space-delimited, and hence,
Excel can read it either way it sees it.
Chart from the Insert menu. Specify that you want an XY
(scatter) chart, and choose one which connects the points by smooth lines.
f(x), and a value x0 near
which the function is believed to vanish, Newton's method allows us to quickly determine
the value x* at which f(x*) = 0. The
method works by following the tangent of the curve of f(x) and computing
its x-intercept. Starting with x0, this leads to successive
approximations of the form: 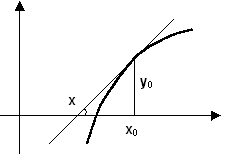 |
x = x0 - f(x0) / f'(x0)
|
x becomes less than EPSILON or the difference
(in abs value) between two successive approximations is less than EPSILON.
To guard against situations in which there is no zero, or the zero is not reachable
from the starting point, we also stop the loop (and declare failure in finding the
zero) if more than 1000 iterations were performed.
We will apply the above technique for solving the following problem: You need to buy a house whose present value is A=$135,000. You don't have that much in cash but you can apply for a 30-year mortgage and make monthly payments. The maximum you can pay each month is $1000. What should the annual interest rate be so that you can afford this house?
We have already seen the mortgage formula, which relates the cash price
A, the amortization period n, the monthly interest
percentage r, and the monthly payment P, but the unknown
now is r. We are therefore interested in finding the zero of
the function f(r), given by:
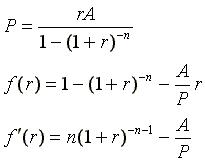
(x2-1)). When run, the
program prompts for an initial value
x0 and then either
outputs the sought zero or state that no zero was found.
EPSILON to 1.E-3. and run. Did you get the
correct zero of the function? If not, debug your program.
EPSILON is changed to 1.E-6?
EPSILON values) and justify the
shown counts.
x0?
(x2+1). Did your program get stuck
in an infinite loop or did it correctly detect the problem?
f(r)
defined above. Note that the independent variable is now called
r, not x, so you need to rename one to the other.